Короткий опис документа:
Демонстрація починається з подання теми уроку. На екрані зображується графік функції y = f (x). На графіку видно, що в точці х = -1 не існує дотичної до графіка, а в х = 0 дотична є паралельною осі Х. Далі демонструється визначення мінімуму функції. У ньому зазначено, що мінімумом функції y = f (x) є х = х0. для якої існує деяка околиця, де для всіх точок околиці справедливо f (x)> f (x0). За допомогою малюнка пояснюється, що існує околиця х = 0 - наприклад, (-0,5; 0,5), в якій всі значення околиці задовольняють умові f (x)> f (0). Робиться зауваження, що мінімум функції не є її найменшим значенням, так як то кажуть про найменшому значенні, коли розглядається вся область визначення. Тому часто унаім. ≠ наминаючи.
Далі представляється теорема, в якій розкривається зв'язок похідної функції і екстремуму. Відзначається, що якщо в даній точці функції є екстремум, то похідна в ній не існує або дорівнює нулю. Очевидно, що при дослідженні функції необхідно відшукати якісь особливі точки. Вводиться поняття стаціонарних і критичних точок. Стаціонарні точки визначаються як точки, що належать області визначення функції, з похідною, яка дорівнює нулю. Критичними точками називають точки області визначення, де функція неперервна, однак похідна не існує.
Розглядається приклад, в якому необхідно побудувати графік функції у = х 2 + 4х-1. Знаючи особливості графіка квадратичної функції, можна відразу сказати, що графіком цієї залежності є парабола з гілками, спрямованими вниз, так як старший коефіцієнт функції негативний. Точкою максимуму функції буде вершина цієї параболи. Дотична до вершини паралельна осі Х, тому в вершині виконується умова у = 0. Знаходимо похідну функції у = (- х 2 + 4х-1) = 2х + 4. Вирішивши рівняння 2х + 4 = 0, отримаємо х = 2. У точці х = 2 значення функції у = 3. Знайдена точка (2; 3) і є вершина параболи. Для побудови параболи вибирається ще дві симетричні точки - наприклад (0; -1) і (4; 0). Тепер зобразити графік даної функції просто.
Далі представляється теорема 2, в якій вказані достатні умови екстремуму. У теоремі зазначено, що для безперервної на проміжку Х функції y = f (x), яка має в цьому проміжку критичну точку х = х0. вірно:
- при існуванні близько критичної точки околиці, де х<х0. f΄(x)<0, а для х>х0 f (x)> 0, то точка - мінімум функції;
- при існуванні близько критичної точки околиці, де х<х0. f΄(x)>0, а для х> х0 f (x) <0, то данная точка есть максимумом функции;
- при існуванні близько критичної точки околиці, де при переході через цю точку знак не змінюється, то екстремуму тут немає.
У прикладі 2 необхідно знайти екстремуми і накреслити графік функції у = 3х 4 -16x 3 + 24х 2 -11. Спочатку визначається похідна f (x) = (3х 4 -16x 3 + 24х 2 -11). Після перетворення похідна приймає вид f (x) = 12х (х-2) 2. Рішення рівняння - х = 0 і х = 2. Дані стаціонарні точки відзначаються на числовій прямій. Також на прямий зазначається, який є функція на кожному з утворених проміжків - зростаючої чи спадаючої. Очевидно, що на проміжку (-∞; 0) функція спадна, так як похідна приймає негативні значення, а на (0; 2) і (2; + ∞) похідна позитивна, функція зростає. У х = 0 функція змінює напрямок з порядку спадання на зростаючу, ця точка - мінімум, в х = 2 не змінюється знак похідної, тому екстремуму в ній немає. Знаходимо в мінімальній точці f (0) = - 11. Відповідно, наминаючи. = -11.
Для побудови графіка необхідно знати стаціонарні, критичні точки. Визначаємо точки перетину функції з координатними осями - це (-1; 0), (1; 0). Враховуємо, що мінімум функції - знайдена (-11; 0). А також стаціонарна точка (2; 5), де дотична паралельна Х - точка перегину. Знайшовши ще кілька координат точок, будується графік функції.
Узагальнюючи вивчене, будується алгоритм дослідження довільної неперервної функції y = f (x). В алгоритмі присутня 4 кроки:
- пошук похідною f (x);
- знаходження критичних, стаціонарних точок;
- побудова особливих точок на координатній прямій - критичних і стаціонарних, вказівка знака похідної на утворилися проміжках;
- висновок про монотонності, екстремальних точках функції.
Окремо виводиться зауваження про необхідність позначки на координатної прямої точок, які звертають в нуль знаменник виду p (x) / q (x). При цьому вказується, що дані крапки не екстремальні.
У прикладі 3 необхідно досліджувати функцію у = (х 2 -3) / (х 2 +1). Функція досліджується згідно з алгоритмом. Спочатку знаходиться похідна f (x) = ((х 2 -3) / (х 2 +1)) '. Скориставшись правилом знаходження похідної приватного, знаходимо похідну f (x) = 8х / (х 2 +1) 2. На координатній прямій вказуємо точку, де похідна дорівнює нулю - х = 0. Далі розставляємо знаки похідної на сформованих проміжках. Очевидно, на проміжку (-∞; 0] функція спадає, а зростаюча вона на [0; + ∞). Судячи з властивостями графіка, точка х = 0 - це мінімум функції, де наминаючи. = -3.
2. Точки екстремуму функції і їх відшукання
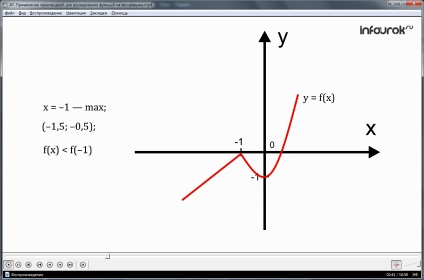
Розглянемо графік функції, зображений на малюнку 1. Дана функція не має дотичній в точці х = -1, а в точці х = 0, вона збігається з віссю у (тобто перпендикулярна осі х).
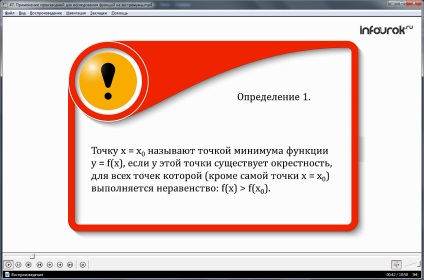
Визначення 1. Точку х = х0 називають точкою мінімуму функції у = f (x), якщо у цієї точки існує околиця, для всіх точок якої (крім самої точки х = х0) виконується нерівність:
Тобто, функція, графік якої показаний на рис. 1, має точку мінімуму х = 0. Так як у даній точки існує околиця, наприклад, або (-0,5; 0,5), для всіх точок якої, крім точки х = 0, виконується нерівність f (x)> f (0). (Еф від ікс більше еф від нуля)
Значення функції в точці мінімуму позначають ymin. (Ігрек мінімум)
Зауваження. Але дане значення не є найменшим значенням функції, так як найменше значення розглядає на всіх області визначення, тобто ymin часто відрізняється від yнаім. (Ігрек найменшого)
Наприклад, функція графік якої зображено на рис. 1, не має найменшого значення, але ymin (мінімальне значення) існує.
Визначення 2. Точку х = х0 називають точкою максимуму функції у = f (x), якщо у цієї точки існує околиця, для всіх точок якої, крім самої точки х = х0. виконується нерівність: f (x) Повернемося до малюнка 1, дана функція, має точку максимуму х = -1. Так як у даній точки існує околиця, наприклад, (-1,5; -0,5), для всіх точок якої, крім точки х = -1, виконується нерівність f (x) Значення функції в точці максимуму позначають ymax. (Ігрек максимальний) Не плутайте це значення з yнаіб. (Ігрек найбільший), тобто з найбільшим значенням функції у всій розглянутій області визначення. Ми можемо стверджувати, що найбільшого значення немає у аналізованої функції, aymax (максимальне значення) існує. Точки мінімуму і максимуму функції об'єднують загальним терміном - точки екстремуму (від латинського слова extremum- «крайній»). Теорема 1. Якщо функція у = f (x) має екстремум в точці х = х0. то в цій точці похідна функції або дорівнює нулю, або не існує. Введемо деякі додаткові позначення: точки області визначення функції, в яких похідна функції дорівнює нулю, називаються стаціонарними. а точки області визначення функції, в яких функція неперервна, але похідна функції не існує, - критичними. Приклад 1. Побудувати графік функції у = х 2 + 4х -1. Рішення. Вам відомо, що графіком заданої квадратичної функції є парабола, причому гілки параболи спрямовані вниз, оскільки коефіцієнт при х 2 від'ємний. Але в такому випадку вершина параболи є точкою максимуму функції, дотична до параболи в її вершині паралельна осі х, значить, в вершині параболи має виконуватися умова у '= 0. (Ігрек штрих дорівнює нулю) Маємо: у '= (- х 2 + 4х -1)' = 2х + 4. Прирівнявши похідну нулю, отримаємо: 2х + 4 = 0; x = 2. Підставивши знайдене значення х в рівняння параболи, отримаємо: у = -2 2 + 4 · 2 -1 = 3. (ігрек дорівнює трьом) Отже, вершиною параболи служить точка (2; 3), а віссю параболи - пряма х = 2. В якості контрольних точок зручно взяти точку (0; -1) і симетричну їй щодо осі параболи точку (4; -1). На рис. 2 по знайденим трьом точкам побудована парабола - графік заданої квадратичної функції. Теорема 2 (достатні умови екстремуму). Нехай функціяy = f (x) неперервна на промежуткеXі має всередині проміжку стаціонарну або критичну точку х = х0. тоді: а) якщо у цієї точки існує така околиця, що в ній при х<х0 выполняется неравенствоf´(х) <0, а при х>х0 - неравенствоf' (x)> 0, то б) якщо у цієї точки існує така околиця, що в ній при х<х0 выполняется неравенствоf´(х)>0, а при х> х0 - неравенствоf' (x)<0, то в) якщо у цієї точки існує така околиця, що в ній і зліва, і справа від точки х0 знаки похідної однакові, то в точці х = х0 екстремуму немає. Приклад 2. а) Знайти точки екстремуму функції у = 3х 4 -16х 3 + 24х 2 -11; б) побудувати графік цієї функції. Рішення, а) Знайдемо похідну даної функції: f'(x) = 12х 3 -48х 2 + 48х f'(x) = 12x (х 2 -4х + 4); f'(x) = 12x (х-2) 2; Похідна звертається в нуль в точках х = 0 і х = 2 - це дві стаціонарні точки заданої функції. На рис. 3 схематично вказані знаки похідної і поведінку функції по проміжкам області визначення: на проміжку (-, 0) похідна негативна, це свідчить про те убуває, на проміжках (0, 2) і (2, +) - позитивна, функція зростає. Точка, х = 0 - точка мінімуму функції, а х = 2 точкою екстремуму не є. У точці мінімуму х = 0 маємо f (0) = -11 (підставили значення х = 0 в аналітичне завдання функції), значить, уmin = -11. б) Щоб побудувати графік функції, потрібно знати особливо важливі точки графіка. До таких належать: - знайдена точка мінімуму (0; -1); - стаціонарна точка х = 2; в цій точці f (x) = 3 • 2 4 -16 • 2 3 + 24 ∙ 2 + 2 -11 = 5; - точки перетину з осями координат; в даному прикладі це вже знайдена точка (0; -11) - точка перетину графіка з віссю у. І ще: можна здогадатися, що f (1) = 0, значить, знайдена точка перетину графіка з віссю х - це точка (1; 0). Отже, ми маємо точку мінімуму (0; -11), точку перетину графіка з віссю х - точку (1; 0) і стаціонарну точку (2; 5). У цій точці дотична до графіка функції горизонтальна, але це не крапка екстремуму, а точка перегину. Графік функції схематично зображено на рис. 4. Зауважимо, що є ще одна точка перетину графіка з віссю абсцис, але знайти її нам не вдалося. Вивчене узагальнимо у вигляді алгоритму.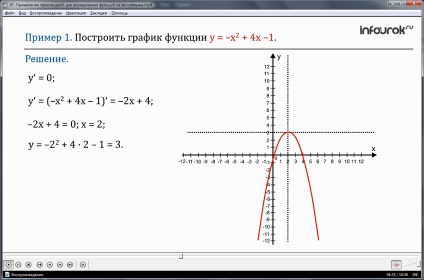
АЛГОРИТМ ДОСЛІДЖЕННЯ безперервної ФУНКЦІЇ y = f (x) HA монотонності і екстремуми
1. Знайти похідну f '(x).
2. Знайти стаціонарні і критичні точки.
3. Відзначити стаціонарні і критичні точки на числовій прямій і визначити знаки похідної на одержані проміжках.
4. Спираючись на теореми, зробити висновки про монотонності функції і про її точках екстремуму.
Зауваження: якщо задана функція має вигляд у = (ігрек дорівнює пе від ікс, поділене на ку від ікс), то на числовій прямій необхідно відзначити точки, в яких знаменник q (x) звертається в нуль, до визначення знаків похідної. Але, дані точки не є точками екстремуму.
Приклад 6. Дослідити функцію у = на монотонність і екстремуми.
Рішення. Зауважимо, що функція всюди неперервна, так як знаменник в будь-якій точці х більше нуля. Скористаємося зазначеним вище алгоритмом.
1) Знайдемо похідну заданої функції:
(Еф штрих від ікс одно вісім ікс, поділене на квадрат суми ікс в квадраті і одиниці).
2) Похідна звертається в нуль в точках х = 0 це стаціонарна точка. Похідна існує при будь-якому х, критичних точок, і точок розриву функції немає.
3) Відзначимо точку 0 на числовій прямій і розставимо знаки похідної на одержані проміжках (рис. 5).
4) Робимо висновки: на промені (-, 0] функція спадає, на промені [0, +) функція зростає.
Далі, х = 0 - точка мінімуму, причому ymin = -3 (ігрек мінімальний дорівнює мінус три) (підставили значення x = 0 в формулу у =).