Тригонометричні функції - це функції кута. особливо корисні при дослідженні та моделюванні періодичних подій. Вони можуть бути визначені як відношення двох сторін трикутника. що містить кут, або як відношення координат точок по колу, або, більш загально, як нескінченні ряди. або як рішення диференціального рівняння.
Наведемо шість базових тригонометричних функцій. Останні чотири визначаються через перші дві. Іншими словами, вони визначеннями, а не самостійними сутностями.
1. Визначення
1.1. геометричне визначення
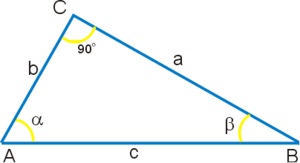
Визначення кутів за допомогою прямокутного трикутника.
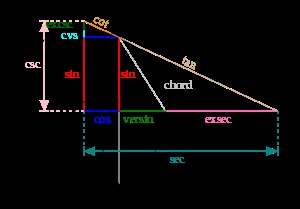
Визначення тригонометричних функцій на одиничному колі.
Тригонометричні функції можна визначити розглянувши прямокутний трикутник.
Косинусом кута називається відношення довжини прилеглого катета до довжини гіпотенузи.
Синусом кута називається відношення довжини протилежного катета до довжини гіпотенузи:
Тангенсом кута називається відношення довжини протилежного катета до довжини прилеглого катета:
Котангенс кута називається відношення довжини прилеглого катета до довжини протилежного катета:
Аналогічним чином можна визначити тригонометричні функції на колі з одиничним радіусом.
1.2. Зв'язок з диференціальним рівнянням
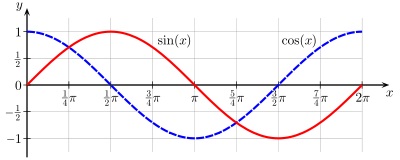
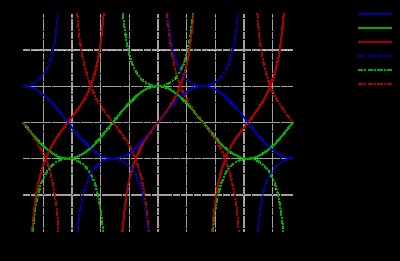
Один період функцій sin (x) і cos (x)
Функції і є рішеннями диференціального рівняння гармонійних коливань
і це періодичні функції з періодом
і мають період
Співвідношення, наведені нижче, дозволяють висловити значення тригонометричних функцій від довільного дійсного аргументу через значення функцій для аргументу з інтервалу
2. Основні співвідношення
Наступне співвідношення випливає з теореми Піфагора.
3. Теореми додавання і формули для кратних кутів
3.1. Формули для функцій суми кутів
З основного співвідношення
3.2. Формули для функцій подвійних кутів
3.3. Формули для функцій потрійних кутів
3.4. Формули для функцій половинних кутів
3.5. Формули для суми функцій кута
3.6. Загальні формули для функцій кратних кутів
Якщо n є цілим позитивним числом, то
4. Загальні формули для ступенів функцій
Якщо n є цілим непарним числом, то
Якщо n є цілим парним числом, то
5. Розклади в ряд Тейлора
Існують такі розклади в ряд Тейлора тригонометричних функцій:
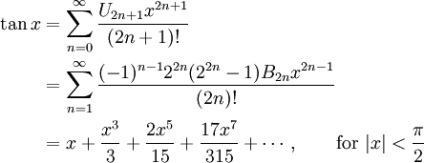
U n n-е перетворення бустрофедон, B n числа Бернуллі. і E n числа Ейлера.
5.1. Зв'язок з експонентою і комплексними числами
Використовуючи вищенаведені розклади в ряди Тейлора можна показати, що функції sin і cos є уявної і дійсної частинами експоненти чисто мнимого числа:
Це співвідношення називається формулою Ейлера.
Можна визначити тригонометричні функції комплексної змінної z:
де i 2 = -1, а і - Відповідно гіперболічні синус і косинус. Для справжнього x мають місце співвідношення