Поверхні, що затягують задані граничні контури
У ряді програм (наприклад, в проектуванні корпусів і крил літаків і кораблів) потрібно будувати гладкі поверхні, що затягують задані остови з кривих - криволінійні сітки, криволінійні напрямні (наприклад, несучий кістяк корпусу корабля), різні граничні контури. У багатьох випадках важливе значення має також і обчислювальна сторона питання - складність обчислення радіус-вектора поверхні і її диференційно-геометричних характеристик не повинна бути занадто високою.
У комп'ютерній геометрії існує кілька різних підходів до вирішення подібних завдань. Нижче буде розглянуто деякі з цих підходів, що стали класичними.
лінійчаті поверхні
Лінійчата поверхню - геометричне місце точок відрізків прямих, що з'єднують відповідні один одному точки двох заданих кривих. Нехай і - дві задані криві. Тоді визначається ними лінійчата поверхня має вигляд
Якщо обидві криві і замкнуті, то лінійчата поверхню замкнута по u. За параметром v лінійчата поверхню завжди незамкнута.
Якщо обидві криві і - відрізки прямих, то лінійчата поверхню називається билинейной і визначається тільки своїми чотирма кутовими точками:
секторіальні поверхні
Секториальная поверхню - окремий випадок лінійчатої поверхні, коли одна з кривих і вироджується в точку:
де - крива, p - точка,
Секториальная билинейная поверхню називається трикутною поверхнею.
поверхні Кунса
Лінійні поверхні Кунса. Віднімемо і додамо до рівняння лінійчатої поверхні рівняння билинейной поверхні, побудованої по чотирьом кутовим точкам (див. Вище). Рівняння лінійчатої поверхні набуде вигляду
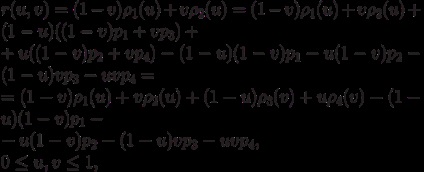
де і - криві, за якими будується дана лінійчата поверхню, причому вважається, що на них обох заданий один і той же параметр і
Підставами тепер в рівняння (6.13) замість відрізків прямих (6.14) рівняння двох довільних кривих і з'єднують відповідно пари точок і Тоді нова поверхня, що задається рівнянням (6.13), буде визначатися чотирма кривими утворюють криволінійний чотирикутник, натягнутий на кутові точки При цьому всі чотири криві увійдуть в рівняння (6.13) симетрично. Вийде лінійна поверхню Кунса.
Визначення 6.3.1. Нехай задані чотири криві, що утворюють криволінійний чотирикутник з кутами в точках:
Функції будемо називати функціями зміщення лінійної поверхні Кунса. Сама лінійна поверхню Кунса визначається наступною формулою:
Зауваження 6.3.1. Лінійна поверхня Кунса не є, взагалі кажучи, лінійчатої поверхнею. Назва "лінійна" обумовлено тим, що в її визначенні використовуються лінійні функції зсуву і
Зауваження 6.3.2. Параметрична область поверхні Кунса може мати вигляд прямокутника, не обов'язково збігається з квадратом
Матричний вигляд рівняння поверхні Кунса. Перетворимо формулу (6.15) до іншого виду. Маємо в матричних позначеннях
Приклад 6.3.1. Задамо за допомогою поверхні Кунса область D площини, обмежену еліпсом або де з півосями Уявімо кордон області D у вигляді чотирьох кривих - дуг еліпса, стикуються в точках Відповідна лінійна поверхню Кунса має вигляд
Перевага завдання плоских областей у вигляді лінійних поверхонь Кунса полягає в тому, що у поверхні Кунса параметрическая область-завжди прямокутник.
Приклад 6.3.2. Поверхня Кунса, побудована за кривими, що лежить на заданих поверхнях. Криві розфарбовані червоним, зеленим, жовтим і помаранчевим.
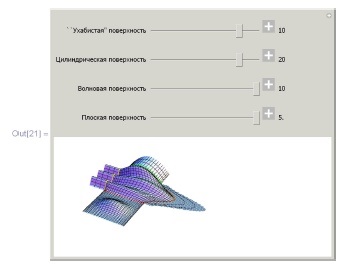
Узагальнені поверхні Кунса. При стикуванні лінійних поверхонь Кунса по граничним кривим похідні в напрямку, ортогональному кордоні, зазнають розрив. Щоб гладко склеювати поверхні Кунса, необхідно будувати їх таким чином, щоб вони мали на кордоні задані (узгоджені) похідні до k -го порядку включно. Похідні в дотичному напрямку визначаються рівняннями самих граничних кривих, а похідні в трансверсальному до кордону напрямку необхідно ставити додатково.
Визначення 6.3.2. Узагальненої поверхнею Кунса n-го порядку називається поверхня
задається чотирма граничними кривими стикуються в точках і а також чистими приватними похідними в трансверсальному напрямку на граничних кривих до -го порядку включно і змішаними приватними похідними в кутових точках до -го порядку включно:
а також узагальненими функціями зміщення де в якості яких можуть бути взяті довільні гладкі функції, що задовольняють співвідношенням