З методом введення нової змінної при вирішенні раціональних рівнянь з однією змінною ви познайомилися в курсі алгебри 8-го класу. Суть цього методу при вирішенні систем рівнянь та ж сама, але з технічної точки зору є деякі особливості, які ми і обговоримо в наступних прикладах.
Приклад 3. Вирішити систему рівнянь
Рішення. Введемо нову змінну Тоді перше рівняння системи можна буде переписати в більш простому вигляді: Вирішимо це рівняння щодо змінної t:

Обидва ці значення задовольняють умові. а тому є корінням раціонального рівняння зі змінною t. Але виходить, або звідки знаходимо, що х = 2у, або
Таким чином, за допомогою методу введення нової змінної нам вдалося як би «розшарувати» перше рівняння системи, досить складне по виду, на два простіших рівняння:
Що ж далі? А далі кожне з двох отриманих простих рівнянь потрібно по черзі розглянути в системі з рівнянням х 2 - у 2 = 3, про який ми поки не згадували. Іншими словами, завдання зводиться до вирішення двох систем рівнянь:
Треба знайти рішення першої системи, другий системи і всі отримані пари значень включити у відповідь. Вирішимо першу систему рівнянь:
Скористаємося методом підстановки, тим більше що тут для нього все готове: підставимо вираз 2у замість х в друге рівняння системи. отримаємо
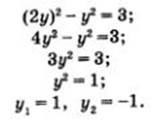
Так як х = 2у, то знаходимо відповідно х1 = 2, х2 = 2. Тим самим отримані два рішення заданої системи: (2; 1) і (-2; -1). Вирішимо другу систему рівнянь:
Знову скористаємося методом підстановки: підставимо вираз 2х замість у в друге рівняння системи. отримаємо
Це рівняння не має коренів, значить, і система рівнянь не має рішень. Таким чином, у відповідь треба включити тільки рішення першої системи.
Метод введення нових змінних при вирішенні систем двох рівнянь з двома змінними застосовується в двох варіантах. Перший варіант: вводиться одна нова змінна і використовується тільки в одному рівнянні системи. Саме так виглядали справи в прикладі 3.Второй варіант: вводяться дві нові змінні і використовуються одночасно в обох рівняннях системи. Так закінчиться справа в прикладі 4.
Приклад 4. Вирішити систему рівнянь